（本题8分）
（1） 求出下列各数：① 2的平方根； ②-27的立方根； ③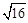
的算术平方根．
（2） 将（1）中求出的每个数准确地表示在数轴上．
（3） 将（1）中求出的每个数按从小到大的顺序排列，并用“﹤”连接．
相关知识点
推荐套卷
（本题8分）
（1） 求出下列各数：① 2的平方根； ②-27的立方根； ③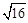的算术平方根．
（2） 将（1）中求出的每个数准确地表示在数轴上．
（3） 将（1）中求出的每个数按从小到大的顺序排列，并用“﹤”连接．
粤公网安备 44130202000953号