(共8分)阅读下列材料:
1×2= 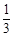 (1×2×3-0×1×2),
(1×2×3-0×1×2),
2×3= 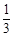 (2×3×4-1×2×3),
(2×3×4-1×2×3),
3×4= 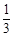 (3×4×5-2×3×4),
(3×4×5-2×3×4),
由以上三个等式相加,可得1×2+2×3+3×4= 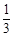 ×3×4×5=20.
×3×4×5=20.
读完以上材料,请你计算下列各题:
(1)1×2+2×3+3×4+…+10×11(写出过程);
(2)1×2+2×3+3×4+…+ n×( n+1)=__________;
(3)1×2×3+2×3×4+3×4×5+…+7×8×9=__________.
相关知识点
推荐套卷

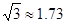 )
)

 ,其中
,其中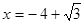 .
. +(2m-1)x+
+(2m-1)x+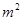 -1经过坐标原点,且当x<0时,y随x的增大而减小.
-1经过坐标原点,且当x<0时,y随x的增大而减小. 粤公网安备 44130202000953号
粤公网安备 44130202000953号