小明在测量铅球的半径时,先将铅球完全浸没在一个带刻度的圆柱形小水桶中,拿出铅球时,小明发现小水桶中的水面下降了4cm,小明测得小水桶的直径为24cm,求铅球的半径(球得体积公式为V=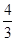 πr3,r为球的半径,结果精确到0.01cm).
πr3,r为球的半径,结果精确到0.01cm).
相关知识点
推荐套卷
小明在测量铅球的半径时,先将铅球完全浸没在一个带刻度的圆柱形小水桶中,拿出铅球时,小明发现小水桶中的水面下降了4cm,小明测得小水桶的直径为24cm,求铅球的半径(球得体积公式为V=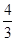 πr3,r为球的半径,结果精确到0.01cm).
πr3,r为球的半径,结果精确到0.01cm).