(本小题满分14分)东华旅行社为某旅游团包飞机去旅游,其中旅行社的包机费为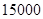 元,旅游团中的每人的飞机票按以下方式与旅行社结算:若旅游团的人数在
元,旅游团中的每人的飞机票按以下方式与旅行社结算:若旅游团的人数在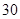 人或
人或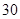 人以下,飞机票每张收费
人以下,飞机票每张收费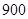 元;若旅游团的人数多于
元;若旅游团的人数多于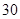 人,则给予优惠,每多
人,则给予优惠,每多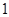 人,机票费每张减少
人,机票费每张减少 元,但旅游团的人数最多有
元,但旅游团的人数最多有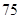 人,设旅游团的人数为
人,设旅游团的人数为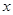 人,每张飞机票价为
人,每张飞机票价为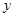 元,旅行社可获得的利润为
元,旅行社可获得的利润为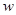 元.
元.
(1)写出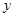 与
与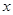 的函数关系式;
的函数关系式;
(2)写出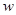 与
与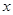 的函数关系式;
的函数关系式;
(3)那么旅游团的人数为多少时,旅行社可获得的利润最大?
推荐套卷
(本小题满分14分)东华旅行社为某旅游团包飞机去旅游,其中旅行社的包机费为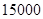 元,旅游团中的每人的飞机票按以下方式与旅行社结算:若旅游团的人数在
元,旅游团中的每人的飞机票按以下方式与旅行社结算:若旅游团的人数在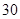 人或
人或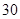 人以下,飞机票每张收费
人以下,飞机票每张收费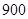 元;若旅游团的人数多于
元;若旅游团的人数多于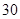 人,则给予优惠,每多
人,则给予优惠,每多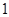 人,机票费每张减少
人,机票费每张减少 元,但旅游团的人数最多有
元,但旅游团的人数最多有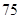 人,设旅游团的人数为
人,设旅游团的人数为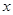 人,每张飞机票价为
人,每张飞机票价为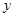 元,旅行社可获得的利润为
元,旅行社可获得的利润为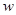 元.
元.
(1)写出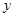 与
与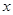 的函数关系式;
的函数关系式;
(2)写出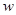 与
与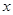 的函数关系式;
的函数关系式;
(3)那么旅游团的人数为多少时,旅行社可获得的利润最大?