设椭圆E的方程为
，点O为坐标原点，点A的坐标为
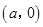，点B的坐标为
，点M在线段AB上，满足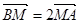
，直线OM的斜率为
.
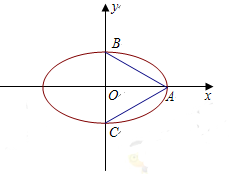
（Ⅰ）求E的离心率e；
（Ⅱ）设点C的坐标为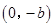
，N为线段AC的中点，点N关于直线AB的对称点的纵坐标为
，求E的方程.
相关试题
，若函数
的最小值是
，
且对称轴是
求
的值；
的最小值.
x|x>a
，集合B＝
A，则实数a的取值范围是a多少？
，且f（1）＝2．
求函数
的最大值和最小值．推荐套卷
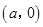设椭圆E的方程为，点O为坐标原点，点A的坐标为，点B的坐标为，点M在线段AB上，满足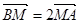，直线OM的斜率为.
（Ⅰ）求E的离心率e；
（Ⅱ）设点C的坐标为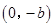，N为线段AC的中点，点N关于直线AB的对称点的纵坐标为，求E的方程.
粤公网安备 44130202000953号