己知圆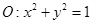 和直线
和直线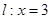 ,在
,在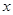 轴上有一点
轴上有一点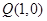 ,在圆
,在圆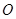 上有不与
上有不与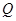 重合的两动点
重合的两动点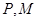 ,设直线
,设直线 斜率为
斜率为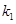 ,直线
,直线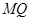 斜率为
斜率为 ,直线
,直线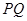 斜率为
斜率为 ,
,
(l)若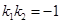
①求出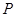 点坐标;
点坐标;
② 交
交 于
于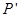 ,
,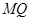 交
交 于
于 ,求证:以
,求证:以 为直径的圆,总过定点,并求出定点坐标.
为直径的圆,总过定点,并求出定点坐标.
(2)若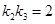 :判断直线
:判断直线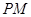 是否经过定点,若有,求出来,若没有,请说明理由.
是否经过定点,若有,求出来,若没有,请说明理由.
相关知识点
推荐套卷
己知圆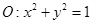 和直线
和直线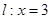 ,在
,在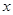 轴上有一点
轴上有一点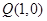 ,在圆
,在圆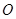 上有不与
上有不与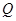 重合的两动点
重合的两动点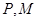 ,设直线
,设直线 斜率为
斜率为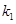 ,直线
,直线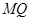 斜率为
斜率为 ,直线
,直线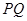 斜率为
斜率为 ,
,
(l)若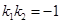
①求出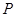 点坐标;
点坐标;
② 交
交 于
于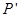 ,
,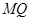 交
交 于
于 ,求证:以
,求证:以 为直径的圆,总过定点,并求出定点坐标.
为直径的圆,总过定点,并求出定点坐标.
(2)若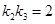 :判断直线
:判断直线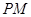 是否经过定点,若有,求出来,若没有,请说明理由.
是否经过定点,若有,求出来,若没有,请说明理由.