甲、乙两个班级进行一次数学考试,按照成绩分为优秀和不优秀两种情况,统计成绩后发现,甲班45名学生中有35人考试成绩不优秀 ,乙班45名学生中有7人考试成绩优秀,试分析:
(1)估计甲班学生数学考试成绩的优秀率
(2)能否有99%的把握认为数学考试成绩优秀与 班级有关?
附: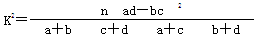 (其中
(其中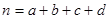 )
)
临界值表
| P(K2≥k) |
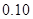 |
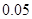 |
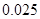 |
 |
 |
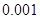 |
| k |
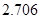 |
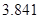 |
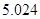 |
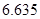 |
 |
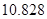 |
推荐套卷
甲、乙两个班级进行一次数学考试,按照成绩分为优秀和不优秀两种情况,统计成绩后发现,甲班45名学生中有35人考试成绩不优秀 ,乙班45名学生中有7人考试成绩优秀,试分析:
(1)估计甲班学生数学考试成绩的优秀率
(2)能否有99%的把握认为数学考试成绩优秀与 班级有关?
附: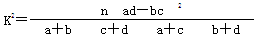 (其中
(其中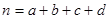 )
)
临界值表
| P(K2≥k) |
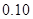 |
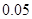 |
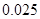 |
 |
 |
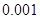 |
| k |
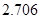 |
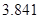 |
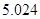 |
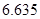 |
 |
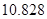 |