如图，在下面的网格图中有一个直角△ABC中，∠ACB=90°，AC=4，BC=3．
（1）请画出将△ABC绕点A按逆时针方向旋转90°后的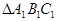
；
（2）若（1）中△ABC的点A、点B坐标分别为（3，5）、（0，1），直接写出（1）中旋转后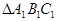的点
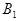坐标是_____________；点
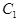坐标是_____________；点B在旋转过程中所经过的路径长是___________;
（3）求出（1）中△ABC扫过的面积．
、
互为相反数，
、
互为倒数，
的绝对值是3，
的值．相关知识点
推荐套卷
如图，在下面的网格图中有一个直角△ABC中，∠ACB=90°，AC=4，BC=3．
（1）请画出将△ABC绕点A按逆时针方向旋转90°后的；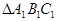
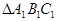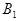（2）若（1）中△ABC的点A、点B坐标分别为（3，5）、（0，1），直接写出（1）中旋转后的点坐标是_____________；点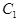坐标是_____________；点B在旋转过程中所经过的路径长是___________;
（3）求出（1）中△ABC扫过的面积．
粤公网安备 44130202000953号