小明从家骑自行车出发,沿一条直路到相距2400m的邮局办事,小明出发的同时,他的爸爸以96m/min速度从邮局同一条道路步行回家,小明在邮局停留2min后沿原路以原速返回,设他们出发后经过t min时,小明与家之间的距离为s1m,小明爸爸与家之间的距离为s2m,图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.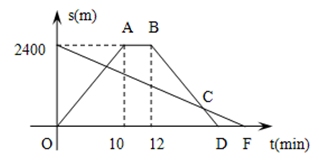
(1)求s2与t之间的函数关系式;
(2)小明从家出发,经过多长时间在返回途中追上爸爸?这时他们距离家还有多远?
相关知识点
推荐套卷

 的中点,P是直径MN上一动点.⊙O的半径为1,问P在直线MN上什么位置时,AP+BP的值最小?并求出AP+BP的最小值.
的中点,P是直径MN上一动点.⊙O的半径为1,问P在直线MN上什么位置时,AP+BP的值最小?并求出AP+BP的最小值.
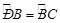 ,试比较线段PC、PD的大小关系.
,试比较线段PC、PD的大小关系.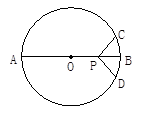
 粤公网安备 44130202000953号
粤公网安备 44130202000953号