如图，把△EFP按图所示的方式放置在菱形ABCD中，使得顶点E、F、P分别在线段AB、AD、AC上.已知EP=FP=
，EF=
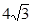，∠BAD=60°，且AB
.
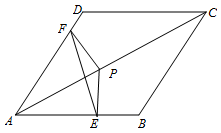
（1）求∠EPF的大小；
（2）若AP=6，求AE+AF的值；
（3）若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动，请直接写出AP长的最大值和最小值.
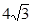如图，把△EFP按图所示的方式放置在菱形ABCD中，使得顶点E、F、P分别在线段AB、AD、AC上.已知EP=FP=，EF=，∠BAD=60°，且AB.
（1）求∠EPF的大小；
（2）若AP=6，求AE+AF的值；
（3）若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动，请直接写出AP长的最大值和最小值.
，其中
，
．
．
．
．
粤公网安备 44130202000953号