某商店购进一批单价为20元的日用品，如果以单价30元销售，那么可卖出400件，如果每提高单价1元，那么销售量Q（件）会减少20，设每件商品售价为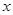
（元）；
（1）请将销售量Q（件）表示成关于每件商品售价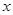（元）的函数；
（2）请问当售价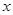（元）为多少，才能使这批商品的总利润
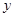（元）最大？
分抛物线
与x轴所围图形为面积相等的两部分，求k的值．
（Ⅰ）讨论
的单调性；
的最大值和最小值．
都是正实数,且
，求证:
.
知抛物线
通过点P(1,1),且在点Q(2,-1)处与直线
相切,求实数
的值.
推荐套卷
某商店购进一批单价为20元的日用品，如果以单价30元销售，那么可卖出400件，如果每提高单价1元，那么销售量Q（件）会减少20，设每件商品售价为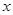（元）；
（1）请将销售量Q（件）表示成关于每件商品售价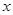（元）的函数；
（2）请问当售价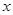（元）为多少，才能使这批商品的总利润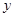（元）最大？
粤公网安备 44130202000953号