（本小题满分12分）如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，PA=AD=1，AB=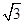
，点E为PD的中点，点F在棱DC上移动。
（1）当点F为DC的中点时，试判断EF与平面PAC的位置关系，并说明理由；
（2）求证：无论点F在DC的何处，都有PF⊥ AE
（3）求二面角E-AC-D的余弦值。
相关试题
}的前
项和为
，
的等差中项，等差数列{
}满足
，
．
，
的通项公式；
，求数列
的前
是等差数列，满足
，数列
满足
，且
为等比数列．
的通项公式；
中，
．
；
数列
的前
的值
且
，求
的取值范围．
//
，求
的值
的值相关知识点
推荐套卷
（本小题满分12分）如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，PA=AD=1，AB=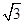，点E为PD的中点，点F在棱DC上移动。
（1）当点F为DC的中点时，试判断EF与平面PAC的位置关系，并说明理由；
（2）求证：无论点F在DC的何处，都有PF⊥ AE
（3）求二面角E-AC-D的余弦值。
粤公网安备 44130202000953号