(本题6分)如图1是用硬纸板做成的两个全等的直角三角形,两直角边的长分别为a和b,斜边长为c,如图2是以c为直角边的等腰直角三角形.请你开动脑筋,将它们拼成一个能证明勾股定理的图形.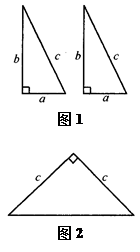
(1)画出拼成的这个图形的示意图;
(2)用这个图形证明勾股定理;
(3)假设图1中的直角三角形有若干个,你能只运用图1中所给的直角三角形拼出另一种能证明勾股定理的图形吗?请画出拼后的示意图(无需证明).
相关知识点
推荐套卷
(本题6分)如图1是用硬纸板做成的两个全等的直角三角形,两直角边的长分别为a和b,斜边长为c,如图2是以c为直角边的等腰直角三角形.请你开动脑筋,将它们拼成一个能证明勾股定理的图形.
(1)画出拼成的这个图形的示意图;
(2)用这个图形证明勾股定理;
(3)假设图1中的直角三角形有若干个,你能只运用图1中所给的直角三角形拼出另一种能证明勾股定理的图形吗?请画出拼后的示意图(无需证明).