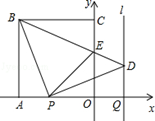
如图,已知二次函数y=ax2+bx+8(a≠0)的图象与x轴交于点A(﹣2,0),B,与y轴交于点C,tan∠ABC=2.
(1)求抛物线的解析式及其顶点D的坐标;
(2)设直线CD交x轴于点E.在线段OB的垂直平分线上是否存在点P,使得经过点P的直线PM垂直于直线CD,且与直线OP的夹角为75°?若存在,求出点P的坐标;若不存在,请说明理由;
(3)过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴向上平移,使抛物线与线段EF总有公共点.试探究:抛物线最多可以向上平移多少个单位长度?
相关知识点
推荐套卷
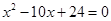 的一个根,求这个三角形的周长.
的一个根,求这个三角形的周长.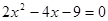 (用配方法解)
(用配方法解)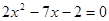
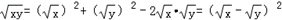 ≥0
≥0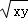 ,当且仅当“x=y”时,等号成立.
,当且仅当“x=y”时,等号成立. +4的最小值.
+4的最小值.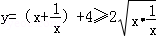 +4=6,当x=
+4=6,当x=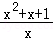 的最小值.
的最小值.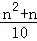 万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用=
万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用= )?最少年平均费用为多少万元?
)?最少年平均费用为多少万元?

 粤公网安备 44130202000953号
粤公网安备 44130202000953号