（本小题满分12分）由于雾霾日趋严重，政府号召市民乘公交出行，但公交车的数量太多会造成资源的浪费，太少又难以满足乘客需求，为此，某市公交公司在某站台的60名候车乘客中进行随机抽样，共抽取10人进行调查反馈，所选乘客情况如下表所示：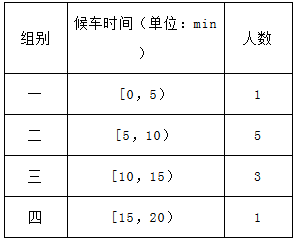
（Ⅰ）估计这60名乘客中候车时间少于10分钟的人数；
（Ⅱ）现从这10人中随机取3人，求至少有一人来自第二组的概率；
（Ⅲ）现从这10人中随机抽取3人进行问卷调查，设这3个人共来自X个组，求X的分布列及数学期望．
相关试题
≥a＋b；
(0<x<1)的最小值．已知函数f(x)＝|x＋3|＋|x－a|(a>0)．
(1)当a＝4时，已知f(x)＝7，求x的取值范围；
(2)若f(x)≥6的解集为{x|x≤－4或x≥2}，求a的值．
设函数f(x)＝|x－1|＋|x－2|.
(1)画出函数y＝f(x)的图象；
(2)若不等式|a＋b|＋|a－b|≥|a|f(x)( a≠0，a，b∈R)恒成立，求实数x的取值范围．
∈A，
∉A.推荐套卷
粤公网安备 44130202000953号