如图直角坐标系中,以M(3,0)为圆心的⊙M交x轴负半轴于A,交x轴正半轴于B,交y轴于C、D.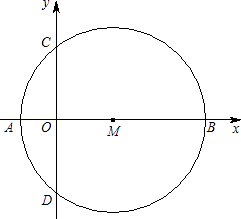
(1)若C点坐标为(0,4),求点A坐标.
(2)在(1)的条件下,在⊙M上,是否存在点P,使∠CPM=45°,若存在,求出满足条件的点P.
(3)过C作⊙M的切线CE,过A作AN⊥CE于F,交⊙M于N,当⊙M的半径大小发生变化时.AN的长度是否变化?若变化,求变化范围,若不变,证明并求值.
相关知识点
推荐套卷
如图直角坐标系中,以M(3,0)为圆心的⊙M交x轴负半轴于A,交x轴正半轴于B,交y轴于C、D.
(1)若C点坐标为(0,4),求点A坐标.
(2)在(1)的条件下,在⊙M上,是否存在点P,使∠CPM=45°,若存在,求出满足条件的点P.
(3)过C作⊙M的切线CE,过A作AN⊥CE于F,交⊙M于N,当⊙M的半径大小发生变化时.AN的长度是否变化?若变化,求变化范围,若不变,证明并求值.