我省教育厅下发了《在全省中小学幼儿园广泛开展节约教育的通知》,通知中要求各学校全面持续开展“光盘行动”.
某市教育局督导检查组为了调查学生对“节约教育”内容的了解程度(程度分为:“A-了解很多”,“B-了解较多”,“C-了解较少”,“D-不了解”),对本市一所中学的学生进行了抽样调查,我们将这次调查的结果绘制了以下两幅统计图.根据以上信息,解答下列问题:
被调查学生对“节约教育”内容了解程度的统计图

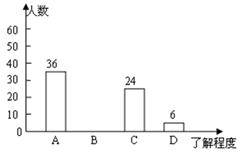
(1)本次抽样调查了多少名学生?
(2)补全两幅统计图;
(3)若该中学共有1800名学生,请你估计这所中学的所有学生中,对“节约教育”内容“了解较多”的有多少名?