某中学拟组织学生开展唱红歌比赛活动.团委对初四一班会唱红歌的学生人数进行了统计(A:会唱1首;B会唱2首;C:会唱3首;D:会唱4首以上),并绘制了如下两幅不完整的统计图.请你根据图中提供的信息解答以下问题:
(1)在条形统计图中,将会唱4首以上的部分补充完整.
(2)求该班会唱1首的学生人数占全班人数的百分比.
(3)在扇形统计图中,计算会唱3首的部分所对应的圆心角的度数.
(4)若该校初四共有350人,请你估计会唱3首红歌的学生约有多少人?
相关知识点
推荐套卷
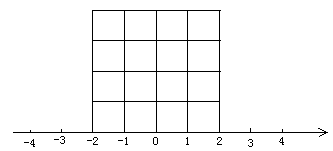
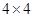 的方格,画出面积为5的正方形并涂上阴影;
的方格,画出面积为5的正方形并涂上阴影;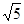 和-
和-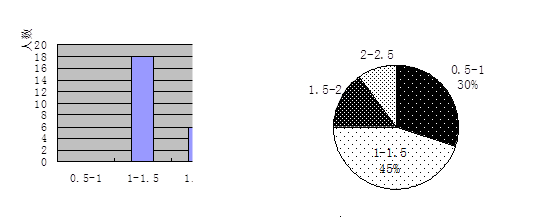
 粤公网安备 44130202000953号
粤公网安备 44130202000953号