如图：已知P是半径为5cm的⊙O内一点．解答下列问题：
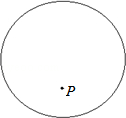
（1）用尺规作图找出圆心O的位置．（要求：保留所有的作图痕迹，不写作法）
（2）用三角板分别画出过点P的最长弦AB和最短弦CD．
（3）已知OP=3cm，过点P的弦中，长度为整数的弦共有_________ 条．
相关试题
cm，求将等腰直角三角形绕直线AC旋转一周所得到图形的面积．
．
相关知识点
推荐套卷
如图：已知P是半径为5cm的⊙O内一点．解答下列问题：
（1）用尺规作图找出圆心O的位置．（要求：保留所有的作图痕迹，不写作法）
（2）用三角板分别画出过点P的最长弦AB和最短弦CD．
（3）已知OP=3cm，过点P的弦中，长度为整数的弦共有_________ 条．
粤公网安备 44130202000953号