(本小题满分13分)一款击鼓小游戏的规则如下:每盘游戏都需击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得-200分).设每次击鼓出现音乐的概率为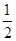 ,且各次击鼓出现音乐相互独立.
,且各次击鼓出现音乐相互独立.
(1)设每盘游戏获得的分数为X,求X的分布列和数学期望E(X).
(2)玩三盘游戏,至少有一盘出现音乐的概率是多少?
相关知识点
推荐套卷
(本小题满分13分)一款击鼓小游戏的规则如下:每盘游戏都需击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得-200分).设每次击鼓出现音乐的概率为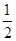 ,且各次击鼓出现音乐相互独立.
,且各次击鼓出现音乐相互独立.
(1)设每盘游戏获得的分数为X,求X的分布列和数学期望E(X).
(2)玩三盘游戏,至少有一盘出现音乐的概率是多少?