如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒.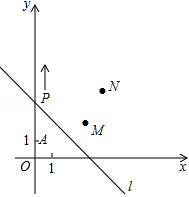
(1)当t=3时,求直线的解析式;
(2)当直线通过点M时,求直线l的解析式;
(3)若点M,N位于l的异侧,确定t的取值范围.
相关知识点
推荐套卷
如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒.
(1)当t=3时,求直线的解析式;
(2)当直线通过点M时,求直线l的解析式;
(3)若点M,N位于l的异侧,确定t的取值范围.