已知椭圆C：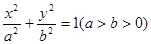
的长轴是短轴的两倍，点
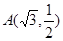在椭圆上．不过原点的直线l与椭圆相交于A、B两点，设直线OA、l、OB的斜率分别为
、
、
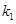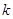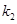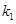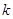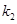，且、、恰好构成等比数列．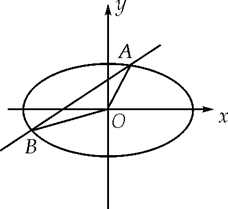
（Ⅰ）求椭圆C的方程．
（Ⅱ）试探究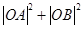
是否为定值？若是，求出这个值；否 则求出它的取值范围．
推荐套卷
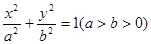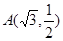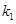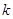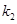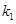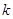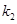已知椭圆C：的长轴是短轴的两倍，点在椭圆上．不过原点的直线l与椭圆相交于A、B两点，设直线OA、l、OB的斜率分别为、、，且、、恰好构成等比数列．
（Ⅰ）求椭圆C的方程．
（Ⅱ）试探究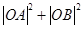是否为定值？若是，求出这个值；否 则求出它的取值范围．
粤公网安备 44130202000953号