(本小题满分16分)已知各项均为正数的等差数列{an}的公差d不等于0,设a1、a3、ak是公比为q的等比数列{bn}的前三项.
(1)若k=7,a1=2.
①求数列{anbn}的前n项和Tn;
②将数列{an}与{bn}中相同的项去掉,剩下的项依次构成新的数列{cn},设其前n项和为Sn,求S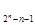 -22n-1+3·2n-1的值;
-22n-1+3·2n-1的值;
(2)若存在m>k,m∈N*使得a1、a3、ak、am成等比数列,求证:k为奇数.
相关知识点
推荐套卷
(本小题满分16分)已知各项均为正数的等差数列{an}的公差d不等于0,设a1、a3、ak是公比为q的等比数列{bn}的前三项.
(1)若k=7,a1=2.
①求数列{anbn}的前n项和Tn;
②将数列{an}与{bn}中相同的项去掉,剩下的项依次构成新的数列{cn},设其前n项和为Sn,求S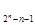 -22n-1+3·2n-1的值;
-22n-1+3·2n-1的值;
(2)若存在m>k,m∈N*使得a1、a3、ak、am成等比数列,求证:k为奇数.