(本小题满分13分)如图,在直三棱柱ABC—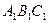 中,
中,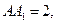 AB = 1,
AB = 1,
 ;点D、E分别在
;点D、E分别在 上,且
上,且 ,
,
四棱锥 与直三棱柱的体积之比为3:5。
与直三棱柱的体积之比为3:5。
(1)求异面直线DE与 的距离;(8分)
的距离;(8分)
(2)若BC = ,求二面角
,求二面角 的平面角的正切值。(5分)
的平面角的正切值。(5分)
|
推荐套卷
(本小题满分13分)如图,在直三棱柱ABC—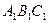 中,
中,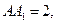 AB = 1,
AB = 1,
 ;点D、E分别在
;点D、E分别在 上,且
上,且 ,
,
四棱锥 与直三棱柱的体积之比为3:5。
与直三棱柱的体积之比为3:5。
(1)求异面直线DE与 的距离;(8分)
的距离;(8分)
(2)若BC = ,求二面角
,求二面角 的平面角的正切值。(5分)
的平面角的正切值。(5分)
|