F1、F2为双曲线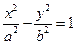 的左右焦点,O为坐标原点,P在双曲线的左支上,点M在右准线上,且满足:
的左右焦点,O为坐标原点,P在双曲线的左支上,点M在右准线上,且满足: ,
, (λ>0)
(λ>0)
(1)求此双曲线的离心率;
(2)若过点N( ,
,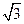 )的双曲线C的虚轴端点分别为B1、B2(B1在y轴正半轴上),点A、B在双曲线上,且
)的双曲线C的虚轴端点分别为B1、B2(B1在y轴正半轴上),点A、B在双曲线上,且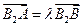 ,
, ,求双曲线C和直线AB的方程。
,求双曲线C和直线AB的方程。
相关知识点
推荐套卷
F1、F2为双曲线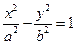 的左右焦点,O为坐标原点,P在双曲线的左支上,点M在右准线上,且满足:
的左右焦点,O为坐标原点,P在双曲线的左支上,点M在右准线上,且满足: ,
, (λ>0)
(λ>0)
(1)求此双曲线的离心率;
(2)若过点N( ,
,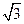 )的双曲线C的虚轴端点分别为B1、B2(B1在y轴正半轴上),点A、B在双曲线上,且
)的双曲线C的虚轴端点分别为B1、B2(B1在y轴正半轴上),点A、B在双曲线上,且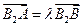 ,
, ,求双曲线C和直线AB的方程。
,求双曲线C和直线AB的方程。