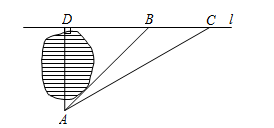
如图，小明家在A处，门前有一口池塘，隔着池塘有一条公路l，AB是A到l的小路. 现新修一条路AC到公路l. 小明测量出∠ACD=30º，∠ABD=45º，BC="50m." 请你帮小明计算他家到公路l的距离AD的长度（精确到0.1m；参考数据：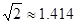
，
）.
，
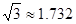，求
的值。整体
，其中，
，
.
相关知识点
推荐套卷
如图，小明家在A处，门前有一口池塘，隔着池塘有一条公路l，AB是A到l的小路. 现新修一条路AC到公路l. 小明测量出∠ACD=30º，∠ABD=45º，BC="50m." 请你帮小明计算他家到公路l的距离AD的长度（精确到0.1m；参考数据：，）.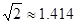
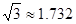粤公网安备 44130202000953号