如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.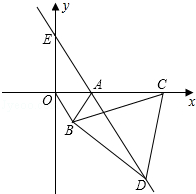
(1)△OBC与△ABD全等吗?判断并证明你的结论;
(2)随着点C位置的变化,点E的位置是否会发生变化?若没有变化,求出点E的坐标;若有变化,请说明理由.
相关知识点
推荐套卷
如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
(1)△OBC与△ABD全等吗?判断并证明你的结论;
(2)随着点C位置的变化,点E的位置是否会发生变化?若没有变化,求出点E的坐标;若有变化,请说明理由.