（本小题共14分）已知抛物线P：x2="2py" （p>0）．
（Ⅰ）若抛物线上点
到焦点F的距离为
．
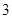（ⅰ）求抛物线
的方程；
（ⅱ）设抛物线的准线与y轴的交点为E，过E作抛物线的切线，求此切线方程；
（Ⅱ）设过焦点F的动直线l交抛物线于A，B两点，连接
，
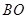并延长分别交抛物线的准线于C，
D两点，求证：以CD为直径的圆过焦点F．
，
．求
和
的值．
，
，
，
，求
的值.
．
的值．
的值；
的值．
．相关知识点
推荐套卷
（本小题共14分）已知抛物线P：x2="2py" （p>0）．
（Ⅰ）若抛物线上点到焦点F的距离为．
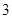（ⅰ）求抛物线的方程；
（ⅱ）设抛物线的准线与y轴的交点为E，过E作抛物线的切线，求此切线方程；
（Ⅱ）设过焦点F的动直线l交抛物线于A，B两点，连接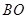，并延长分别交抛物线的准线于C，
D两点，求证：以CD为直径的圆过焦点F．
粤公网安备 44130202000953号