（本小题满分12分）（文）已知函数f（x）=x（x+a）-lnx，其中a为常数．
（1）当a=-1时，求f（x）的极值；
（2）若f（x）是区间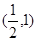
内的单调函数，求实数a的取值范围；
（3）过坐标原点可以作几条直线与曲线y=f（x）相切？请说明理由．
相关试题
,
的奇偶性并用定义证明；
时，总有
成立，求
的取值范围.
是定义域在
的函数，且
，对于任意的实数
，都有
，当
>0时，
.
的值；
在
，解不等式
.推荐套卷
（本小题满分12分）（文）已知函数f（x）=x（x+a）-lnx，其中a为常数．
（1）当a=-1时，求f（x）的极值；
（2）若f（x）是区间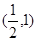内的单调函数，求实数a的取值范围；
（3）过坐标原点可以作几条直线与曲线y=f（x）相切？请说明理由．
粤公网安备 44130202000953号