如图，在四边形ABCD中，点P是边BC上一动点，过点P作直线EF∥AB，且与∠ABC、∠CBG的角平分线分别相交于点E、F．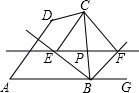
（1）求证：EP=FP；
（2）当点P运动到BC边的中点时，四边形BFCE是什么特殊的四边形？说明理由；
（3）如果四边形BFCE是正方形，求∠ABC的度数．
(2) 
x2+1 )]，其中x= —
；
； (4) 
；
．相关知识点
推荐套卷
如图，在四边形ABCD中，点P是边BC上一动点，过点P作直线EF∥AB，且与∠ABC、∠CBG的角平分线分别相交于点E、F．
（1）求证：EP=FP；
（2）当点P运动到BC边的中点时，四边形BFCE是什么特殊的四边形？说明理由；
（3）如果四边形BFCE是正方形，求∠ABC的度数．
粤公网安备 44130202000953号