（本小题共13分）某厂生产的产品在出厂前都要做质量检测，每一件一等品都能通过检测，每一件二等品通过检测的概率为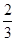
．现有10件产品，其中6件是一等品，4件是二等品．
（Ⅰ） 随机选取1件产品，求能够通过检测的概率；
（Ⅱ） 随机选取3件产品，其中一等品的件数记为
，求的分布列；
（Ⅲ） 随机选取3件产品，求这三件产品都不能通过检测的概率．
，
，
时，求函数
的最大值；
，且
在
的取值范围.
中，
，
，
；
，求证：数列
是等差数列.
，
，
，且
，
时，求
的值；
求
的取值范围.
，
，求
.
，且
，求：
的值；
的值.推荐套卷
（本小题共13分）某厂生产的产品在出厂前都要做质量检测，每一件一等品都能通过检测，每一件二等品通过检测的概率为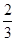．现有10件产品，其中6件是一等品，4件是二等品．
（Ⅰ） 随机选取1件产品，求能够通过检测的概率；
（Ⅱ） 随机选取3件产品，其中一等品的件数记为，求的分布列；
（Ⅲ） 随机选取3件产品，求这三件产品都不能通过检测的概率．
粤公网安备 44130202000953号