已知:如图,四边形ABCD中,∠C=90°,∠ABD=∠CBD,AB=CB,P是BD上一点,PE⊥BC,PF⊥CD,垂足分别为E、F.
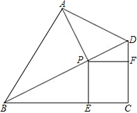
(1)若PA的值2,求EF的值;
(2)若BD=10,P是BD的中点,sin∠BAP=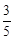 ,求四边形PECF的面积.
,求四边形PECF的面积.
相关知识点
推荐套卷
已知:如图,四边形ABCD中,∠C=90°,∠ABD=∠CBD,AB=CB,P是BD上一点,PE⊥BC,PF⊥CD,垂足分别为E、F.

(1)若PA的值2,求EF的值;
(2)若BD=10,P是BD的中点,sin∠BAP=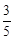 ,求四边形PECF的面积.
,求四边形PECF的面积.