在一个布口袋里装着白、红、黑三种颜色的小球,它们除颜色之外没有任何其它区别,其中有白球3只、红球2只、黑球1只.袋中的球已经搅匀.
(1)闭上眼睛随机地从袋中取出1只球,求取出的球是黑球的概率;
(2)若取出的第1只球是红球,将它放在桌上,闭上眼睛从袋中余下的球中再随机地取出1只球,这时取出的球还是红球的概率是多少?
(3)若取出一只球,将它放回袋中,闭上眼睛从袋中再随机地取出1只球,两次取出的球都是白球概率是多少?(用列表法或树状图法计算)
相关知识点
推荐套卷
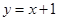 的图象与反比例函数
的图象与反比例函数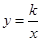 (
(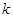 为常数,且
为常数,且 )的图象都经过点A(m,2).
)的图象都经过点A(m,2).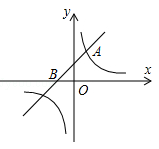
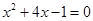 ,求代数式
,求代数式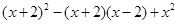 的值.
的值.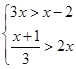 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号