为鼓励创业,市政府制定了小型企业的优惠政策,许多小型企业应运而生,某镇统计了该镇1-5月新注册小型企业的数量,并将结果绘制成如下两种不完整的统计图:

(1)某镇今年1-5月新注册小型企业一共有 家.请将折线统计图补充完整;
(2)该镇今年3月新注册的小型企业中,只有2家是餐饮企业,现从3月新注册的小型企业中随机抽取2家企业了解其经营状况,请用列表或画树状图的方法求出所抽取的2家企业恰好都是餐饮企业的概率.
相关知识点
推荐套卷

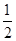 .
. ÷(2x —
÷(2x — 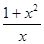 )其中,x=
)其中,x=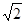 +1
+1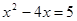 (2)计算:
(2)计算: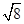 +(-1)3-2×
+(-1)3-2×
 粤公网安备 44130202000953号
粤公网安备 44130202000953号