已知抛物线y=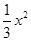 +bx+c与直线BC相交于B、C两点,且B(6,0)、C(0,3).
+bx+c与直线BC相交于B、C两点,且B(6,0)、C(0,3).

(1)填空:b= ,c= ;
(2)长度为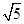 的线段DE在线段CB上移动,点G与点F在上述抛物线上,且线段EF与DG始终平行于y轴.
的线段DE在线段CB上移动,点G与点F在上述抛物线上,且线段EF与DG始终平行于y轴.
①连结FG,求四边形DGFE的面积的最大值,并求出此时点D的坐标;
②在线段DE移动的过程中,是否存在DE=GF?若存在,请直接写出此时点D的坐标;若不存在,试说明理由.
相关知识点
推荐套卷

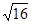 +
+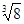 -丨-5丨
-丨-5丨
 (k>0,x>0)的图象与AB相交于点D,与BC相交于点E,且BE=CE.
(k>0,x>0)的图象与AB相交于点D,与BC相交于点E,且BE=CE.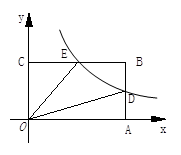
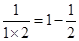
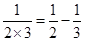
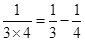 ┅┅
┅┅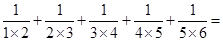 .
.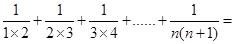 .(用含有
.(用含有 的式子表示)
的式子表示)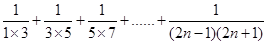 的值为
的值为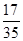 ,求
,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号