某研究性学习小组，为了测量某池塘边A、B两点间的距离，让一架航模在直线AB的正上方24米的高度飞行，当航模位于点D处时，在A点处测得航模仰角为60°，5分钟后，当航模在点C处时，在B点测得航模仰角为45°，己知航模飞行的速度为每分钟45米，试计算A、B两点的距离．（结果精确到0．1米，参考数据：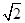
=1．41，
=1．73．）
相关试题
为
边的中点，连结DE并延长DE交AB延长线于F. 求证：
．
中，当 
＝1时， 
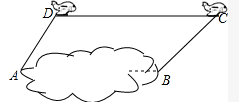
＝－2；当相关知识点
推荐套卷
某研究性学习小组，为了测量某池塘边A、B两点间的距离，让一架航模在直线AB的正上方24米的高度飞行，当航模位于点D处时，在A点处测得航模仰角为60°，5分钟后，当航模在点C处时，在B点测得航模仰角为45°，己知航模飞行的速度为每分钟45米，试计算A、B两点的距离．（结果精确到0．1米，参考数据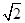：=1．41，=1．73．）
粤公网安备 44130202000953号