如图,在一笔直的海岸线上有A、B两个观测点,B在A的正东方向,AB=4km.从A测得灯塔C在北偏东60°的方向,从B测得灯塔C在北偏西27°的方向,求灯塔C与观测点A的距离(精确到0.1km).
(参考数据:sin27°≈0.45,cos27°≈0.90,tan27°≈0.50, ≈1.73)
≈1.73)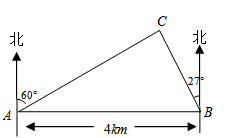
相关知识点
推荐套卷
如图,在一笔直的海岸线上有A、B两个观测点,B在A的正东方向,AB=4km.从A测得灯塔C在北偏东60°的方向,从B测得灯塔C在北偏西27°的方向,求灯塔C与观测点A的距离(精确到0.1km).
(参考数据:sin27°≈0.45,cos27°≈0.90,tan27°≈0.50, ≈1.73)
≈1.73)