(本小题满分14分)围建一个面积为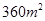 的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修,可供利用的旧墙足够长),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽
的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修,可供利用的旧墙足够长),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽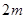 的进出口,如图2所示.已知旧墙的维修费用为
的进出口,如图2所示.已知旧墙的维修费用为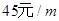 ,新墙的造价为
,新墙的造价为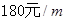 .设利用旧墙的长度为
.设利用旧墙的长度为 (单位:
(单位: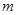 ),修建此矩形场地围墙的总费用为
),修建此矩形场地围墙的总费用为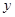 (单位:元).
(单位:元).
(1)将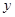 表示为
表示为 的函数,并写出此函数的定义域;
的函数,并写出此函数的定义域;
(2)若要求用于维修旧墙的费用不得超过修建此矩形场地围墙的总费用的15%,试确定 ,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
推荐套卷
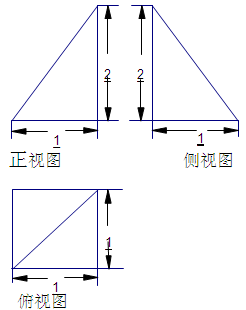
 的三视图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图如下图所示,其中正视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.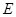 是侧棱
是侧棱 上的动点.
上的动点.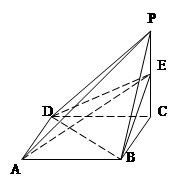
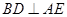 ;
;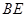 与平面
与平面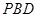 所成角的正弦值;
所成角的正弦值; 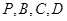 在同一球面上,求该球的体积.
在同一球面上,求该球的体积.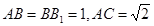 ,直线B1C与平面ABC成45°角.
,直线B1C与平面ABC成45°角.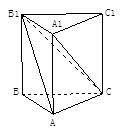

 在
在 方向上的投影.
方向上的投影. 中,
中,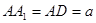 ,
,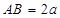 ,
, 、
、  分别为
分别为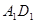 、
、 的中点.
的中点.
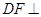 平面
平面 ;
; 平面
平面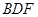 .
.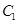 的方程为
的方程为 ,双曲线
,双曲线 的左、右焦点分别为
的左、右焦点分别为 与椭圆
与椭圆 (其中O为原点),求
(其中O为原点),求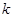 的取值范围。
的取值范围。 粤公网安备 44130202000953号
粤公网安备 44130202000953号