在△ABC中,BA=BC,∠BAC=α,M是AC的中点,P是线段BM上的动点,将线段PA绕点P顺时针旋转2α转得到线段PQ.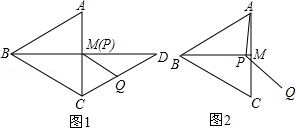
(1)若α=60°且点P与点M重合(如图1),线段CQ的延长线交射线BM于点D.求∠CDB的度数;
(2)在图2中,点P不与点B,M重合,线段CQ的延长线于射线BM交于点D,求∠CDB的大小(用含α的代数式表示);
(3)对于适当大小的α,当点P在线段BM上运动到某一位置(不与点B,M重合)时,能使得线段CQ的延长线与射线BM交于点D,且PQ=QD,请求α的取值范围.
相关知识点
推荐套卷


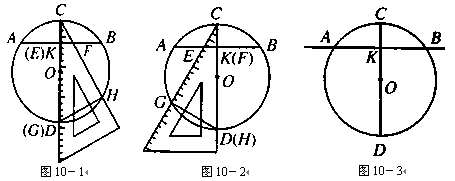
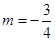 时,求方程的正根.
时,求方程的正根. 粤公网安备 44130202000953号
粤公网安备 44130202000953号