如图,在⊙O的内接△ABC中,AD⊥BC于D,
(1)①若作直径AP,求证:AB·AC=AD·AP;
②已知AB+AC=12,AD=3,设⊙O的半径为y,AB的长为x.求y与x的函数关系式,及自变量x的取值范围;
(2)图2中,点E为⊙O上一点,且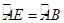 ,求证:CE+CD=BD.
,求证:CE+CD=BD.
推荐套卷
如图,在⊙O的内接△ABC中,AD⊥BC于D,
(1)①若作直径AP,求证:AB·AC=AD·AP;
②已知AB+AC=12,AD=3,设⊙O的半径为y,AB的长为x.求y与x的函数关系式,及自变量x的取值范围;
(2)图2中,点E为⊙O上一点,且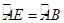 ,求证:CE+CD=BD.
,求证:CE+CD=BD.