如图，抛物线y=-x2+bx+c的顶点为D，与x轴交于A（-1，0）、B（3，0），与y轴交于点C．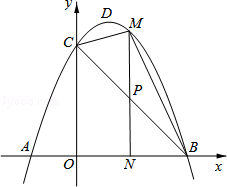
（1）求该抛物线的解析式；
（2）若点P为线段BC上的一点（不与B、C重合），PM∥y轴，且PM交抛物线于点M，交x轴于点N，当四边形OBMC的面积最大时，求△BPN的周长；
（3）在（2）的条件下，当四边形OBMC的面积最大时，在抛物线的对称轴上是否存在点Q，使得△CNQ为直角三角形？若存在，直接写出点Q的坐标．
相关试题
在□ABCD中，对角线AC、BD交于点O，过点O作直线EF分别交线段AD、BC于点E、F．
(1)根据题意，画出图形，并标上正确的字母；
(2)求证：DE＝BF．
如图，在平行四边形ABCD中，DE⊥AB于E，DF⊥BC于F，平行四边形ABCD的周长为48，DE＝5，DF＝10．
(1)求AB的长度；
(2)求平行四边形ABCD的面积．
相关知识点
推荐套卷
粤公网安备 44130202000953号