如图,已知Rt△ABC中,∠C=90°,AC=8,BC=6,点P以每秒1个单位的速度从A向C运动,同时点Q以每秒2个单位的速度从A→B→C方向运动,它们到C点后都停止运动,设点P,Q运动的时间为t秒.
(1)在运动过程中,求P,Q两点间距离的最大值;
(2)经过t秒的运动,求△ABC被直线PQ扫过的面积S与时间t的函数关系式;
(3)P,Q两点在运动过程中,是否存在时间t,使得△PQC为等腰三角形?若存在,求出此时的t值;若不存在,请说明理由( ≈2.24,结果保留一位小数)
≈2.24,结果保留一位小数)
相关知识点
推荐套卷
 =
=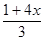 -1
-1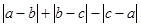
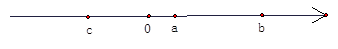
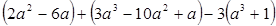 其中
其中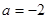
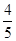 少20人,
少20人, 粤公网安备 44130202000953号
粤公网安备 44130202000953号