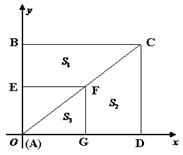
如图,折叠矩形OABC的一边BC,使点C落在OA边的点D处,已知折痕BE=5 ,且
,且 ,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l:y=-
,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l:y=- +c经过点E,且与AB边相交于点F.
+c经过点E,且与AB边相交于点F.
(1)求证:△ABD∽△ODE;
(2)若M是BE的中点,连接MF,求证:MF⊥BD;
(3)P是线段BC上一点,点Q在抛物线l上,且始终满足PD⊥DQ,在点P运动过程中,能否使得PD=DQ?若能,求出所有符合条件的Q点坐标;若不能,请说明理由.
相关知识点
推荐套卷
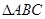 中,
中,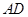 是边
是边 上的中线,过点
上的中线,过点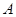 作
作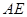 ∥
∥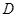 作
作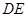 ∥
∥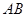 ,
,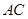 、
、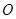 、点
、点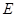 ,连接
,连接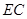 .
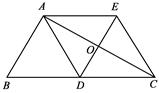
.
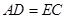 ;
;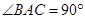 时,求证:四边形
时,求证:四边形 是菱形.
是菱形.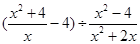 .
.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号