如图,以矩形ABCD的顶点A为原点,AD所在的直线为x轴,AB所在的直线为y轴,建立平面直角坐标系.点D的坐标为(8,0),点B的坐标为(0,6),点F在对角线AC上运动(点F不与点A、C重合),过点F分别作x轴、y轴的垂线,垂足为G、E.设四边形BCFE的面积为S1,四边形CDGF的面积为S2,△AFG的面积为S3.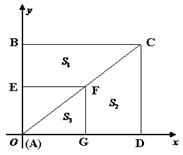
(1)试判断S1、S2,的关系,并加以证明;
(2)当S3:S1=1:3时,求点F的坐标;
(3)如图,在(2)的条件下,把△AEF沿对角线AC所在直线平移,得到△A’E’F’,且A’、F’两点始终在直线AC上,是否存在这样的点E’,使点E’到x轴的距离与到y轴的距离比是5:4.若存在,请求出点E’的坐标;若不存在,请说明理由.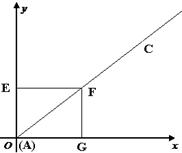
相关知识点
推荐套卷

 = ;
= ; .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号