某同学参加语、数、外三门课程的考试，设该同学语、数、外取得优秀成绩的概率分别为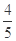
，m，n（m>n），设该同学三门课程都取得优秀成绩的概率为
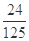，都未取得优秀成绩的概率为
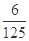，且不同课程是否取得优秀成绩相互独立．
（1）求m，n；
（2）设X为该同学取得优秀成绩的课程门数，求EX．
相关试题
，
为给定的整数，
. 对任意
，作
，集合
，求
型五方连块？
，其中
，且
．求
的最大值和最小值．
、
分别是
的外接圆和内切圆；证明：过
，都可作一个三角形
，使得
的外接圆和内切圆．
的所有排列
的集合为
；
，记
，
；求
．（其中
的元素个数）．推荐套卷
某同学参加语、数、外三门课程的考试，设该同学语、数、外取得优秀成绩的概率分别为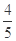，m，n（m>n），设该同学三门课程都取得优秀成绩的概率为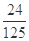，都未取得优秀成绩的概率为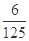，且不同课程是否取得优秀成绩相互独立．
（1）求m，n；
（2）设X为该同学取得优秀成绩的课程门数，求EX．
粤公网安备 44130202000953号