某学校开展“科技创新大赛”活动,设计遥控车沿直线轨道做匀速直线运动
的模型.现在甲、乙两车同时分别从不同起点A,B出发,沿同一轨道到达C处.设t后甲、乙两遥控车与B处的距离分别为d1,d2,且d1,d2与t的函数关系如图,若甲的速度是乙的速度的1.5倍,试根据图象解决下列问题: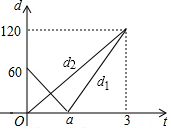
(1)填空:乙的速度是 米/分;
(2)写出d1与t的函数关系式;
(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探求什么时间两遥控车的信号不会产生相互干扰?
相关知识点
推荐套卷
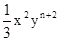 是同类项,求m,n.
是同类项,求m,n.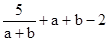 的值.
的值. 时,求代数式(2m-3n)(m+n)+
时,求代数式(2m-3n)(m+n)+ 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号