在我市开展的“阳光体育”跳绳活动中,为了了解中学生跳绳活动的开展情况,随机抽查了全市七年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制两个不完整的统计图.请根据图中提供的信息,解答下列问题:
(1)本次共抽查了多少名学生?
(2)请补全频数分布直方图空缺部分,其中扇形统计图中表示跳绳次数范围135≤x<155的扇形的圆心角度数为 度.
(3)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全市28000名七年级学生中有多少名学生的成绩为优秀?
相关知识点
推荐套卷
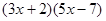 .
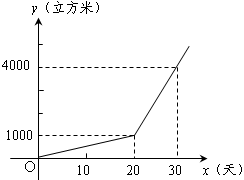
.
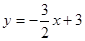 ,请你画出它的图象,并根据图象求:
,请你画出它的图象,并根据图象求: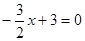 的解;
的解;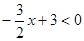 的解集;
的解集;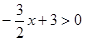 的解集.
的解集.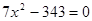 ;(2)
;(2)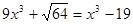
 粤公网安备 44130202000953号
粤公网安备 44130202000953号