如图，在四棱锥P一ABCD中，平面PAD⊥平面ABCD，AB∥DC，
△PAD是等边三角形，已知AD=4，BD=
，AB=2CD=8．
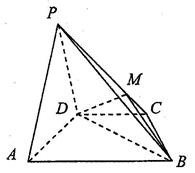
（1）设M是PC上的一点，证明：平面MBD⊥平面PAD；
（2）当M点位于线段PC什么位置时，PA∥平面MBD?请证明你的结论；
（3）求四棱锥P—ABCD的体积．
相关试题
、
、
，且
，
，
，则
、
、
中至少有一个不小于0.
|
,
∈N+}，集合B={
|
,
∈N+}，试证：A
B．
推荐套卷
如图，在四棱锥P一ABCD中，平面PAD⊥平面ABCD，AB∥DC，
△PAD是等边三角形，已知AD=4，BD=，AB=2CD=8．
（1）设M是PC上的一点，证明：平面MBD⊥平面PAD；
（2）当M点位于线段PC什么位置时，PA∥平面MBD?请证明你的结论；
（3）求四棱锥P—ABCD的体积．
粤公网安备 44130202000953号