已知点(1,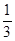 )是函数
)是函数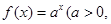 且
且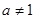 )的图象上一点,等比数列
)的图象上一点,等比数列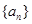 的前n项和为
的前n项和为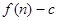 ,数列
,数列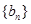
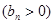 的首项为c,且前n项和
的首项为c,且前n项和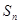 满足
满足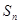 -
-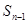 =
=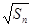 +
+ (n
(n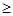 2).
2).
(1)求数列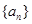 和
和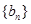 的通项公式;
的通项公式;
(2)若数列{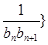 前n项和为
前n项和为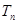 ,问
,问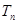 >
>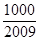 的最小正整数n是多少?
的最小正整数n是多少?
相关知识点
推荐套卷
已知点(1,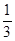 )是函数
)是函数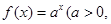 且
且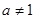 )的图象上一点,等比数列
)的图象上一点,等比数列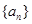 的前n项和为
的前n项和为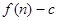 ,数列
,数列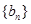
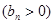 的首项为c,且前n项和
的首项为c,且前n项和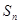 满足
满足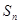 -
-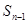 =
=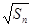 +
+ (n
(n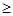 2).
2).
(1)求数列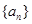 和
和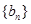 的通项公式;
的通项公式;
(2)若数列{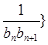 前n项和为
前n项和为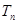 ,问
,问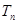 >
>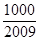 的最小正整数n是多少?
的最小正整数n是多少?