如图，己知抛物线y=k（x+1）（x-3k）（且k＞0）与x轴分别交于A、B两点，A点在B点左边，与Y轴交于C点，连接BC，过A点作AE∥CB交抛物线于E点，0为坐标原点．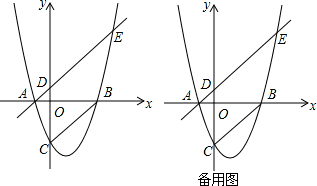
（1）用k表示点C的坐标（0， ）；
（2）若k=1，连接BE，
①求出点E的坐标；
②在x轴上找点P，使以P、B、C为顶点的三角形与△ABE相似，求出P点坐标；
（3）若在直线AE上存在唯一的一点Q，连接OQ、BQ，使OQ⊥BQ，求k的值．
相关试题
－
b)－3(2a
，b=4．在等边△ABC中，点E在AB上，点D在CB的延长线上，且ED=EC.
(1)、若点E是AB的中点，如图1，求证：AE=DB.
(2)、若点E不是AB的中点时，如图2，试确定线段AE与DB的大小关系，并写出证明过程.
如图，在平面直角坐标系
中，△ABC与△DEF全等，其中A、B、C的对应顶点分别为D、E、F，且AB="BC." 若A点的坐标为（
，1），B、C两点的纵坐标均为，D、E两点在
轴上.
(1)、求证：等腰△BCA两腰上的高相等；
(2)、求△BCA两腰上高线的长；
(3)、求△DEF的高线FP的长.
相关知识点
推荐套卷
粤公网安备 44130202000953号